Régression logistique : fichier ‘spam’
Les données
source :
http://archive.ics.uci.edu/ml/index.php
http://archive.ics.uci.edu/ml/machine-learning-databases/spambase/
Extrait des informations du fichier :
- Creators: Mark Hopkins, Erik Reeber, George Forman, Jaap Suermondt Hewlett-Packard Labs, 1501 Page Mill Rd., Palo Alto, CA 94304
- Donor: George Forman (gforman at nospam hpl.hp.com) 650-857-7835
-
Generated: June-July 1999
Informations principales sur la structure de données :
Attribute Information:
# The last column of 'spambase.data' denotes whether the e-mail was
# considered spam (1) or not (0), i.e. unsolicited commercial e-mail.
# Most of the attributes indicate whether a particular word or
# character was frequently occuring in the e-mail. The run-length
# attributes (55-57) measure the length of sequences of consecutive
# capital letters. For the statistical measures of each attribute,
# see the end of this file. Here are the definitions of the attributes:
#
# 48 continuous real [0,100] attributes of type word_freq_WORD
# = percentage of words in the e-mail that match WORD,
# i.e. 100 * (number of times the WORD appears in the e-mail) /
# total number of words in e-mail. A "word" in this case is any
# string of alphanumeric characters bounded by non-alphanumeric
# characters or end-of-string.
#
# 6 continuous real [0,100] attributes of type char_freq_CHAR
# = percentage of characters in the e-mail that match CHAR,
# i.e. 100 * (number of CHAR occurences) / total characters in e-mail
#
# 1 continuous real [1,...] attribute of type capital_run_length_average
# = average length of uninterrupted sequences of capital letters
#
# 1 continuous integer [1,...] attribute of type capital_run_length_longest
# = length of longest uninterrupted sequence of capital letters
#
# 1 continuous integer [1,...] attribute of type capital_run_length_total
# = sum of length of uninterrupted sequences of capital letters
# = total number of capital letters in the e-mail
#
# 1 nominal {0,1} class attribute of type spam
# = denotes whether the e-mail was considered spam (1) or not (0),
# i.e. unsolicited commercial e-mail.
#
#
# 8. Missing Attribute Values: None
#
# 9. Class Distribution:
# Spam 1813 (39.4%)
# Non-Spam 2788 (60.6%)Pour résumer, le fichier se compose de 54 colonnes reprsentant des fréquences d’apparation d’un mot (“wf_hp” pour le mot “hp”) ou la fréquence d’un caractère spécial (“cf_dollar” pour le caractère “$”). Enfin nous avons 3 colonnes liées aux caractères en majuscule et la variable réponse (spam “1”, non spam “0”).
Analyse descriptive
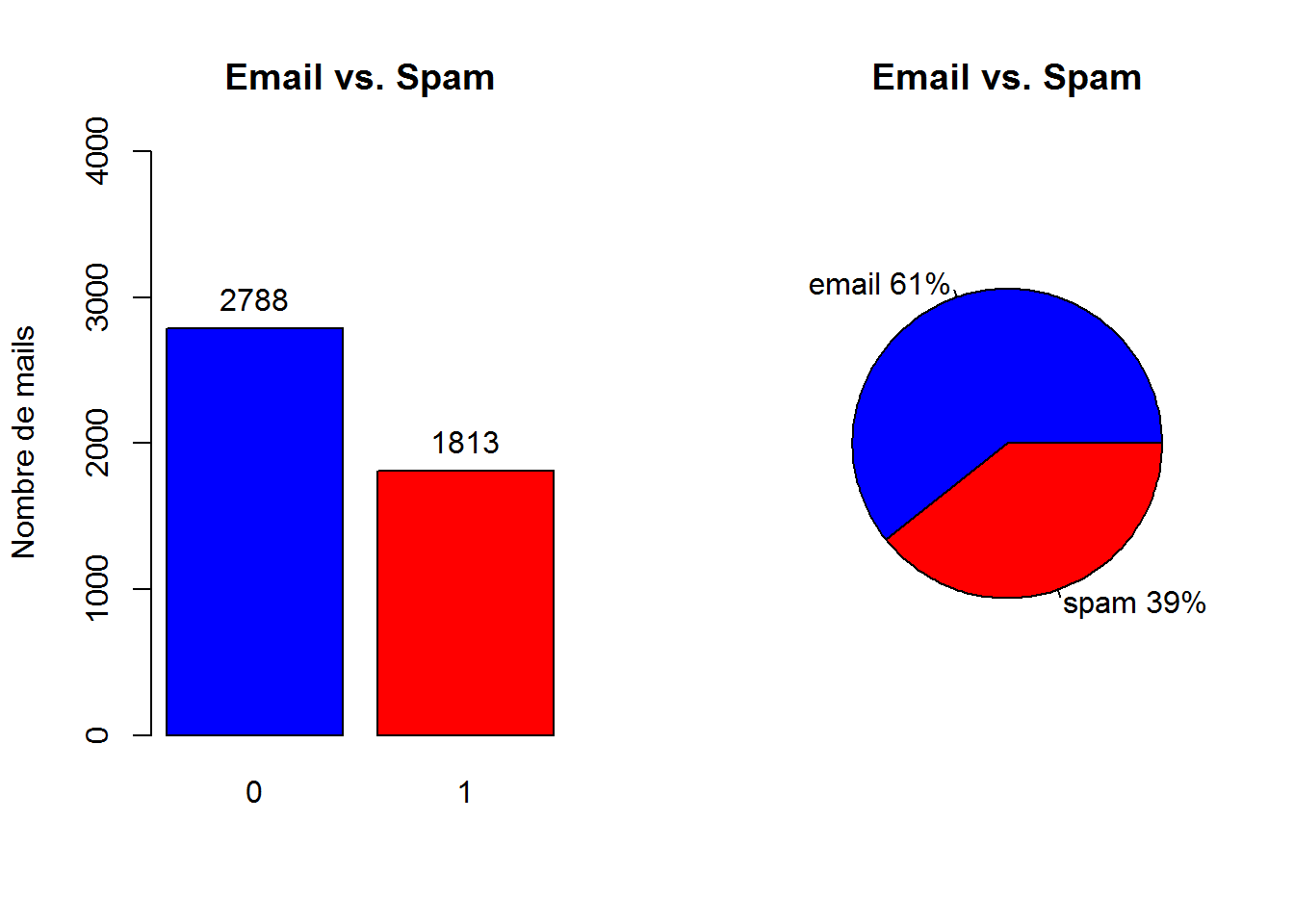
Proportion Mail/Spam :
Moyenne des frequences des mots/caracteres par type de mail spam/non spam : 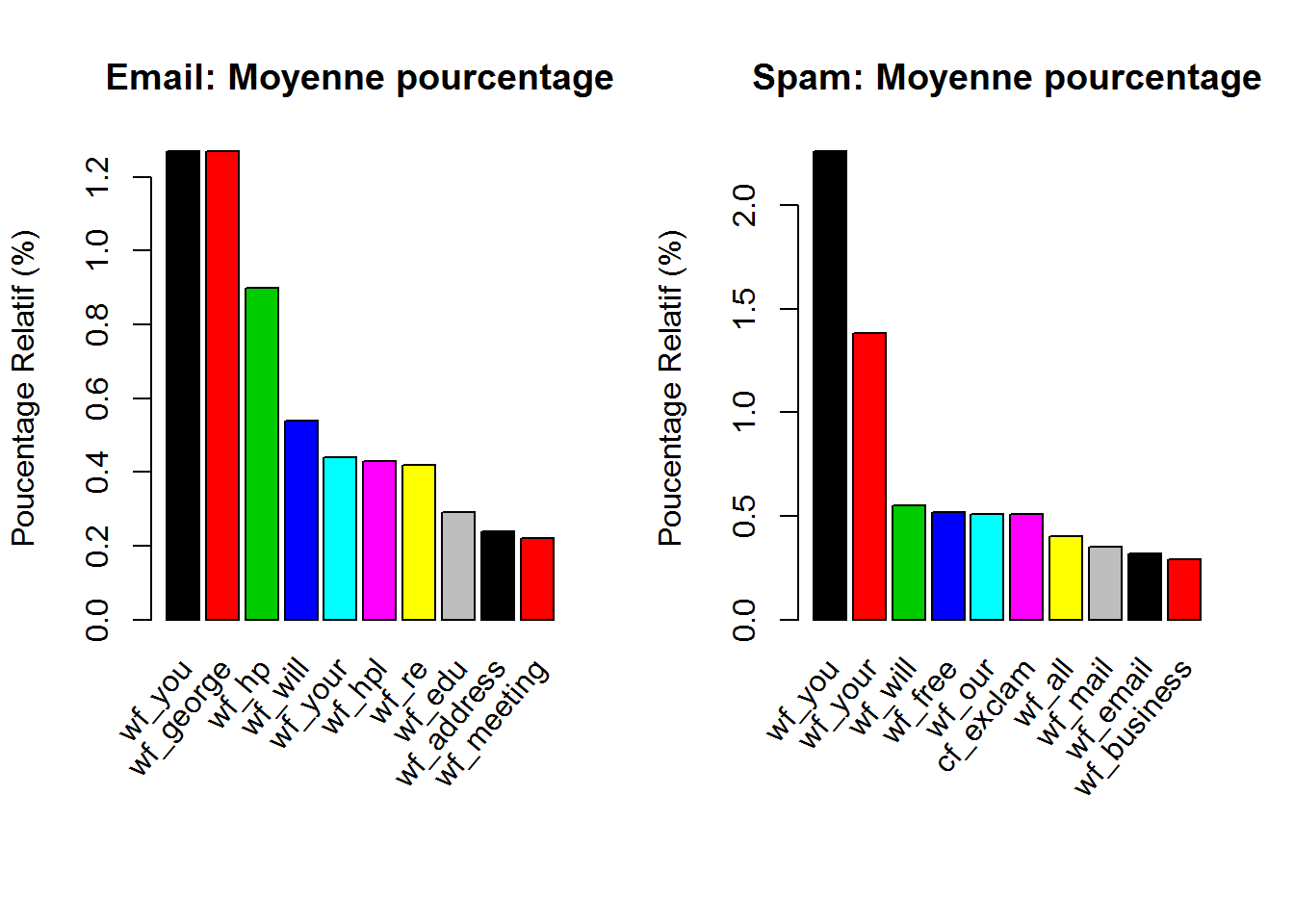
Partie modélisation
Présentation des notations et rappels théoriques
Notations :
\(X=(1,X_{1},...,X_{p})'\), vecteur aléatoire de dimension \(p+1\).
Les marginales \(X_{j}\) sont les variables explicatives.
Soit \(x=(1,x_{1},...,x_{p})'\), une réalisation de \(X\).
\(Y\) variable à expliquer (univariée).
\((X_{1},Y_{1}),...,(X_{n},Y_{n})\) un échantillon aléatoire (iid et de même loi que le couple \((X,Y)\)) tel que \(X_{i}=(1,X_{i1},...,X_{ip})'\).
\((x_{1},y_{1}),...,(x_{n},y_{n})\) une réalisation de \((X_{1},Y_{1}),...,(X_{n},Y_{n})\).
\(X\) matrice des observations :
\(\begin{matrix} 1 & x_{11} \cdots & x_{1p} \\ \vdots & & \vdots \\ 1 & x_{n1}\cdots & x_{np} \end{matrix}\)
Rappels sur le modèle linéaire :
On cherche à expliquer une variable \(Y\) par \(p\) variables \(X=(1,X_{1},...,X_{p})'\). Le but est de modéliser la dépendance de la variable réponse \(Y\) sur les variables explicatives \(X_{1},...,X_{p}\).
Les aspects de la modélisation :
- La description : décrire la relation entre \(Y\) et \(X\)
- L’évaluation : les contributions relatives de chaque prédicteur pour expliquer \(Y\)
-
La prédiction : prévoir la valeur de \(Y\) pour les nouvelles valeurs de \(X\)
Le modèle linéaire s’écrit :
\(Y=X'\beta + \epsilon = \beta_{0}+\beta_{1}X_{1}+...+\beta_{p}X_{p}+\epsilon\)
Avec
\(\beta=(\beta_{0},\beta_{1},...,\beta_{p})' \in \mathbb{R}^{p+1}\) et \(\epsilon=N(0,\sigma^2)\) \(Y\sim N(X'\beta,\sigma^2)\) (hypothèse d’homoscédasticité)
Dans le cas d’une variable \(Y\) qualitative (état, sexe, couleur), l’enjeu est d’expliquer l’appartenance d’un individu à un groupe à partir des \(p\) variables (on parlera de discrimination).
⚠⚠⚠
Contrairement à la régression linéaire, ici on ne peut pas modéliser directement une relation linéaire entre \(Y\) et \(X\).
⚠⚠⚠
On va s’interesser aux probabilités \(P(Y=g_{k}|X=x)\). Pour simplifier, prenons le cas ou \(Y\) est binaire (0 ou 1). De fait, si l’on connait \(P(Y=1|X=x)\) on connait \(P(Y=0|X=x)\).
On peut envisager une relation de la forme :
\(p_{\beta}(x)=\beta_{0}+\beta_{1}X_{1}+...+\beta_{p}X_{p}+\epsilon=X'\beta+\epsilon\)
Ici l’hypothèse d’homoscedasticité des résidus est non vérifiée. En effet, la variance de \(Y|X = p_{\beta}(x)*(1-p_{\beta}(x))\) (non constante).
Egalement, à ce stade nous n’avons pas de restriction sur les valeurs des \(\beta\) et donc des valeurs de \(p_{\beta}(x)\) \((p_{\beta}(x)\in\mathbb{R})\).
Application de la régression logistique
Dans notre cas, nous voulons expliquer la variable \(Y\) (spam “1” ou non spam “0”) par \(p\) variables explicatives \(X=(1,X_{1},...,X_{p})'\).
Le modèle logistique propose une modélisation de la loi de \(Y|X=x\) par une loi de Bernouilli de paramètre \(p_{\beta}(x)=P_{\beta}(Y=1|X=x)\) telle que :
\(log(\frac{p_{\beta}(x)}{1-p_{\beta}(x)})=\beta_{0}+\beta_{1}X_{1}+...+\beta_{p}X_{p}=x'\beta\)
ou encore \(logit \space p_{\beta}(x)=x'\beta\)
\(logit\) désignant la fonction bijective et dérivable de \(]0 \space 1[\) dans \(\mathbb{R}:p \to log(p/1-p)\)
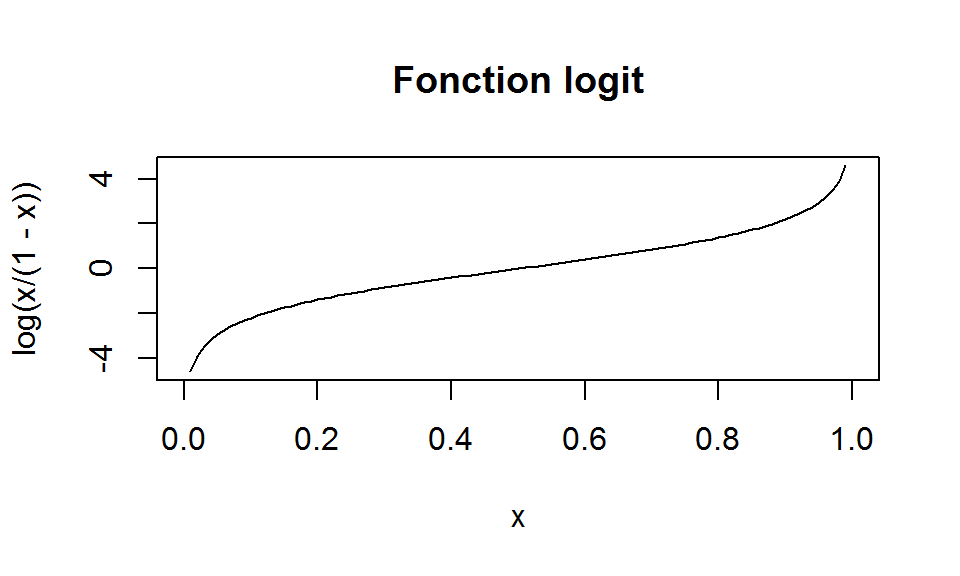
L’égalité peut s’écrire :
\(P_{\beta}(Y=1|X=x)=\frac{\mathrm{e}^{x'\beta}}{1+\mathrm{e}^{x'\beta}}\)
On a
\(\left\{\begin{array}{l}\mathrm{Var_{\beta}[Y|X=x]}=P_{\beta}(Y=1|X=x)*(1-P_{\beta}(Y=1|X=x))\\\mathrm{E_{\beta}[Y|X=x]}=P_{\beta}(Y=1|X=x)\\\end{array}\right.\)
Ce qui implique que la variance n’est pas constante et varie selon \(x\).
Pour une nouvelle mesure \(x\) effectuée, le modèle log linéaire va donc prédire la valeur \(\mathrm{e}^{x'\beta}\) (\(\beta\) est le paramètre à estimer).
Estimation des paramètres par maximum de vraissemblance
La vraissemblance s’écrit :
\(L_{n}(\beta)=\prod_{i=1}^n P_{\beta}(Y=y_{i}|X=x_{i})\)
\(L_{n}(\beta)=\prod_{i=1}^n P_{\beta}(x_{i})^{y_{i}}*(1-P_{\beta}(x_{i}))^{1-y_{i}}\)
La log vraissemblance s’écrit :
\(\mathcal{L}_{n}(\beta)=\sum_{i=1}^n \{ y_{i}*log(P_{\beta}(x_{i}))+(1-y_{i})*log(1-P_{\beta}(x_{i})) \}\)
L’estimateur du maximum de vraissemblance si il existe est solution de l’équation (équation de score):
\(S(\beta)= \nabla\mathcal{L}_{n}(\beta)=X'(Y-P_{\beta})=0\)
Ces équations forment un système non linéaire en \(\beta\). Il faut utiliser des méthodes numériques (algorithme de convergene).
Algorithme IRLS
L’algorithme IRLS (Iterative Reweighted Least Square), dit aussi méthode Newton-Raphson, permet de résoudre ces équations de score.
Il existe aussi l’algorithme de score de Fisher, mais nous allons rester sur IRLS car c’est celui qui est implémenté sous R dans la fonction glm() (method=“glm.fit”).
- choix du point départ \(\beta_{0}\)
- on calcule \(\beta^{k+1}\) à partir de \(\beta^{k}\)
\(\beta^{k+1}=\beta^{k}+A^k\nabla\mathcal{L}_{n}(\beta^k)\)
Où
\(\nabla\mathcal{L}_{n}(\beta^k)\) est le gradient au point \(\beta^{k}\) et \(A^k=-(\nabla^2\mathcal{L}_{n}(\beta^k))^{-1}\) est la matrice de “pas” (inverse du hessien au point \(\beta^{k}\)).
Ecriture matricielle :
\(\beta^{k+1} = \beta^{k}+(X'W_{\beta^k}X)^{-1}X'(Y-P_{\beta^k})\)
Où \(W_{\beta}\) est la matrice diagolane \(P_{\beta}(x_{i})*(1-P_{\beta}(x_{i}))\).
Interprétation des coefficients \(\beta\) :
On peut reprénsenter la fonction \(x \mapsto \frac{\mathrm{e}^{x'\beta}}{1+\mathrm{e}^{x'\beta}}\) pour différentes valeurs de \(\beta\).

Lorsque le \(\beta\) est faibe (proche de 0), on peut voir que la fonction couvre une large valeur de \(x\) autour de 0.5. La discrimintation est difficile. Au contraire si le \(\beta\) est élevé, la zone autour de 0.5 diminue au profit des valeurs extrêmes 0 et 1, ce qui pourrait minimiser les erreurs de prévisions.
Partie modélisation Rstudio
La régression logistique sera exécutée à l’aide de la fonction glm {stats}.
L’exécution se fera dans un premier temps sur le fichier complet afin de présenter le modèle (Utilisation d’un échantillon train/test par la suite).
Présentation du modèle glm
Le modèle :
####
#REGRESSION LOGISTIQUE
####
#execution du modele complet:
modele.reg.log <- glm(Don_spam$spam ~ .,
family = binomial(link="logit"), data=Don_spam)
# Degrees of Freedom: 4600 Total (i.e. Null); 4543 Residual
# Null Deviance: 6170
# Residual Deviance: 1816 AIC: 1932Résultat du modèle :
Application du modele sur les 4601 individus et 58 colonnes (57 + constante)
Le modèle nous fournit en sortie les valeurs des coefficients \(\beta\) par variable.
Les degrés de liberté, (n-1 pour la dimension totale et n-p-1 pour les résidus).
La déviance du modèle seulement avec la constante (Null Deviance), la déviance du modèle et l’AIC.
Calcul de la déviance et de l’AIC d’un modèle M :
\(D_{\mathcal{M}}=-2*\mathcal{L}_{n}(\beta)\)
\(AIC(\mathcal{M})=2*p-2*\mathcal{L}_{n}(\beta)\)
Revenons sur le vecteur \(\beta\), le vecteur des coefficients des descripteurs du modèle.
modele.summary<-summary(modele.reg.log)
# Coefficients:
# Estimate Std. Error z value Pr(>|z|)
# (Intercept) -1.569e+00 1.420e-01 -11.044 < 2e-16 ***
# wf_make -3.895e-01 2.315e-01 -1.683 0.092388 .
# wf_address -1.458e-01 6.928e-02 -2.104 0.035362 *
# wf_all 1.141e-01 1.103e-01 1.035 0.300759
# wf_3d 2.252e+00 1.507e+00 1.494 0.135168
# wf_our 5.624e-01 1.018e-01 5.524 3.31e-08 ***
# wf_over 8.830e-01 2.498e-01 3.534 0.000409 ***
# wf_remove 2.279e+00 3.328e-01 6.846 7.57e-12 ***
# ...En sortie de la commande summary(modele.reg.log), nous avons les valeurs des coefficients et les ecarts type. Nous avons également la valeur du test de Wald avec la p-value associée.
Enfin, le modèle glm nous fournit les valeurs prédites/estimées \(P_{\beta}(Y=y|X=x)=\frac{\mathrm{e}^{x'\beta}}{1+\mathrm{e}^{x'\beta}}\)
p.estime<-modele.reg.log$fitted.values
# 1 2 3 4 5 6 7 8
# 6.189824e-01 9.880333e-01 9.999977e-01 7.786119e-01 7.785570e-01 6.686157e-01 7.612542e-01 6.663679e-01 L’objet “fitted.values” du modèle retourne le vecteur des probabilités d’appartenir à la classe “spam” 1 ou “non spam” 0.Cela nous permettra par la suite d’établir le taux d’erreur des “mal classés” du modèle.
Evaluation du modèle
Afin de mieux comprendre les sorties du modèle glm, je vais détailler la partie “présentation du modèle glm”. En effet, nous allons voir qu’il existe bon nombre d’indicateurs et tests permettant d’évaluer la relation entre \(Y\) et \(X\).
Nous avons vu précedemment avec les estimateurs du maximum de vraissemblance et l’algorithme IRLS que nous obtenons un vecteur \(\beta\) solution de l’équation de score \(S(\beta)=0\). Le vecteur \(\beta\) nous garantit une vraissemblance maximum et donc une déviance minimum pour le modèle.
Modèle Vs modèle trivial
Dans un premier temps, il possible d’opposer la vraissemblance du modele \(L_\mathcal{M}\) et celle du modèle trivial \(L_0\). Des indicateurs existent (pseudos R²) dont le R² de Mc Fadden. Cet indicateur est analogue au R² en régression multiple et s’écrit :
\(R^2_{MF}=1-\frac{LL_\mathcal{M}}{LL_0} \space \left\{\begin{array}{l} Min=0 \space si \space LL_\mathcal{M} = LL_0 \space(pas \space mieux \space que \space modele \space trivial)\\ Max=1 \space si \space LL_\mathcal{M}=0 \space (modele \space parfait)\\\end{array}\right.\)
R2.mf = 1-(modele.reg.log$deviance/modele.reg.log$null.deviance) ; R2.mf## [1] 0.7057179On constate que le modèle “complet” (avec tous les descripteurs) se démarque déja très bien du modèle trivial.Peut-on deja conclure à une bonne discrimination du modèle ?
Pouvoir discriminant du modèle
De façon simple, il est possible de visualiser la répartition des \(P_β\) (nos estimations/prédictions).
#HISTOGRAMME GROUPE
y <- modele.reg.log$fitted.values
y2 <- Don_spam$spam
yb <- hist(y,plot=F)
yc <- tapply(y,y2,cut,breaks=yb$breaks)
tab <- do.call("rbind",lapply(yc,table))
barplot(tab,beside=T,xlab="Répartition des PI",ylab="Fréquence des PI",col=rownames(tab))
legend("top",rownames(tab),cex =0.8,fill=rownames(tab),title="Email=0 Vs Spam=1")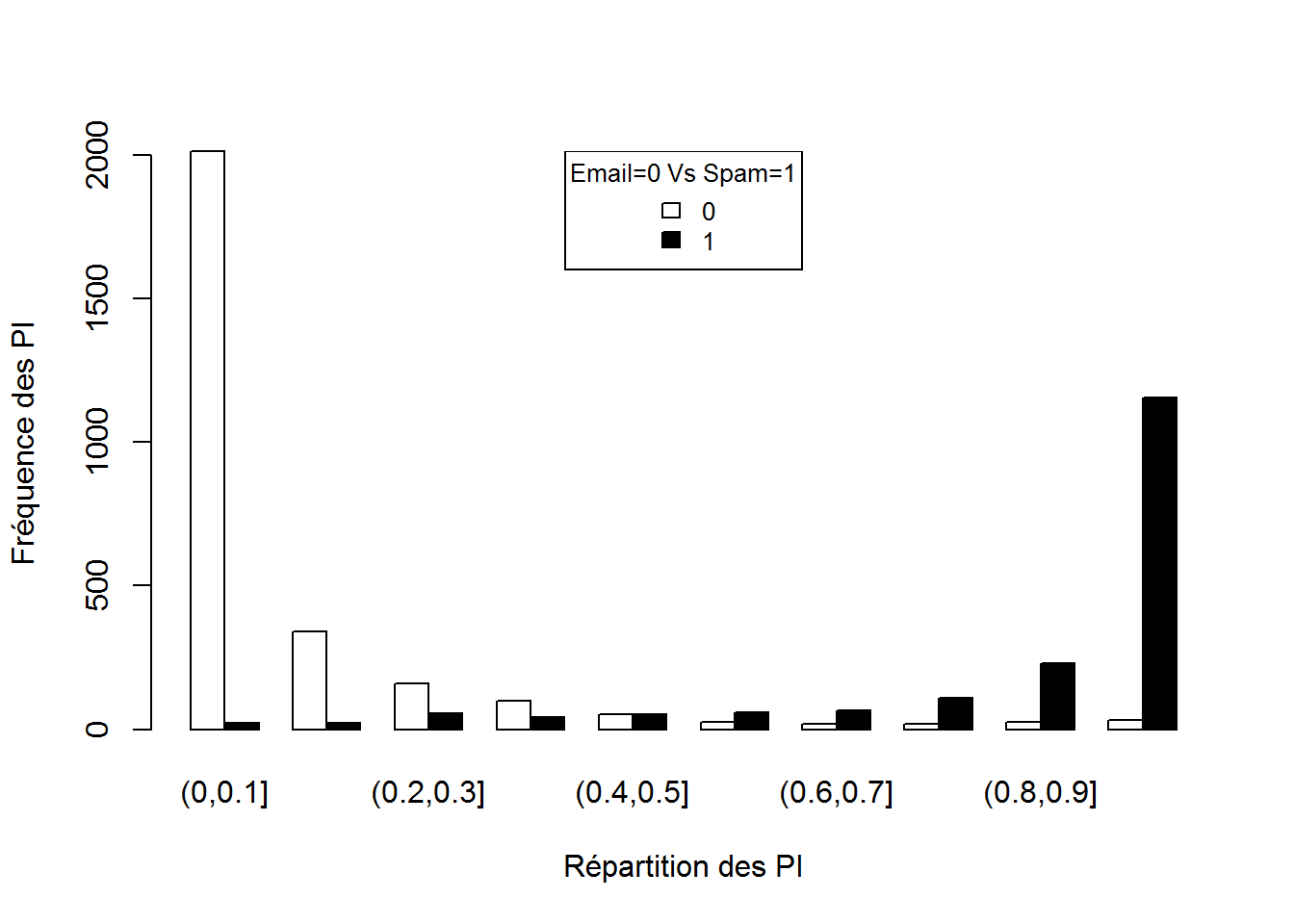
La discrimination des individus semble bonne, la répartition des \(P_β(x_i)\) en fonction de la classe des individus semble également fonctionner.
On peut aller un peu plus loin tout en restant dans la simplicité. Les \(P_β(x_i)\) peuvent être représentés à l’aide d’un diagramme dit de fiabilité. Le diagramme de fiabilité consiste à créer des intervalles, y calculer la somme des positifs et la moyenne des scores.Dans le cas parfait, si les scores sont bien calibrés, les points sont alignés sur une droite \(y=x\).
###Diagramme de fiabilite
breaksMean=function(Piest,Y,n)
#la moyenne de Piest et Y sur chaque intervalle.
{
h=1/n
x=Piest
cl=vector("numeric",length=n+1)
means=matrix("numeric",nrow=2,ncol=n)
#borne gauche 0
cl[1]=0
#calcul des bornes de classes
for(i in 1:n) {cl[i+1]=cl[i]+h
means[1,i]=mean(x[(x<cl[i+1])&(x>=cl[i])])
means[2,i]=mean(Y[(x<cl[i+1])&(x>=cl[i])])
}
return(means)
}
var.reponse = as.numeric(as.vector.factor(Don_spam$spam))
par(mfrow = c(2, 2))
param=c(8,10,20,50)
for(i in 1:4){
res.fiabilite = breaksMean(modele.reg.log$fitted.values,var.reponse,param[i])
#Diagramme de fiabilite
plot(res.fiabilite[1,],res.fiabilite[2,],col="blue",pch=17,type="b",main=paste("Diagramme de fiabilite",dim(res.fiabilite)[2], "classes")
,xlab="Moyennes des scores",ylab="Moyenne des '+'",xlim=c(0,1),ylim=c(0,1))
points(c(0,1),c(0,1),type="l", col="red")
}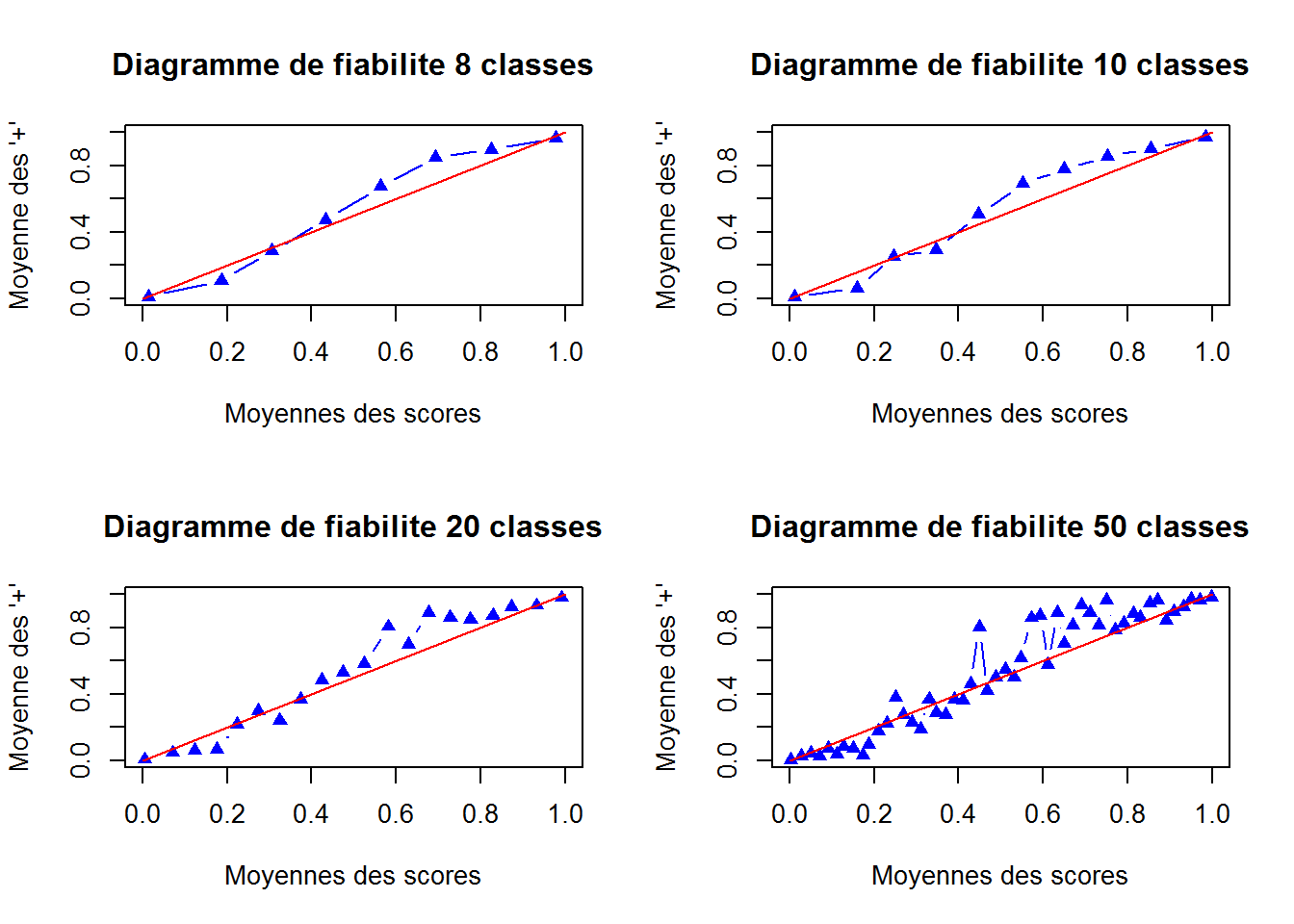
Plus le nombre d’intervalles augmente et moins la moyenne des scores est lissée. On peut voir que globalement, pour un nombre raisonnable d’intervalles, les points suivent la bissectrice.
Il existe également des tests statistiques permettant de quantifier la qualité des scores \(P_β(x_i)\). Il existe le test d’Hosmer et celui de Mann-Whitney. Le test d’Hosmer mesure à l’aide d’un ki2 si les scores (probabilitées attendues) diffèrent des probabilitées théoriques. Le test de Mann-Whitney (basé sur les rangs) mesure si les distributions sont confondues à l’aide d’une loi normale.
library(ResourceSelection)
# il faut des eff de classes superieurs a 5
#(H0), la statistique C suit approximativement une loi du χ2 à (G − 2) (les probas attendus ne different pas des theoriques)
hosm.t = hoslem.test(var.reponse, modele.reg.log$fitted.values) ; hosm.t##
## Hosmer and Lemeshow goodness of fit (GOF) test
##
## data: var.reponse, modele.reg.log$fitted.values
## X-squared = 1725.7, df = 8, p-value < 2.2e-16Si la p-value est inférieur au seuil de risque fixé (prenons 5%), les probabilités prévues diffèrent des probabilités observées. Ici on rejette H0 car la p-value est très faible (p-value < 2.2e-16) et donc les scores diffèrent des scores attendus et le modèle n’est pas validé.
Essayons une autre fonction d’un autre pakage.
library(generalhoslem)
logitgof(Don_spam$spam, modele.reg.log$fitted.values, g =10, ord = FALSE)## Warning in logitgof(Don_spam$spam, modele.reg.log$fitted.values, g = 10, :
## At least one cell in the expected frequencies table is < 1. Chi-square
## approximation may be incorrect.##
## Hosmer and Lemeshow test (binary model)
##
## data: Don_spam$spam, modele.reg.log$fitted.values
## X-squared = 1725.7, df = 8, p-value < 2.2e-16On peut donc conlcure le rejet de H0, le modèle avec ce test n’est pas validé. Le test d’Hosmer est toutefois critiqué et doit être utilisé avec “prudence”.
hosm.t$expected##
## cutyhat yhat0 yhat1
## [2.22e-16,2.45e-13] 4.610000e+02 2.051634e-12
## (2.45e-13,1.42e-05] 4.599993e+02 6.872967e-04
## (1.42e-05,0.00373] 4.595866e+02 4.134381e-01
## (0.00373,0.0456] 4.512903e+02 8.709656e+00
## (0.0456,0.18] 4.069927e+02 5.300730e+01
## (0.18,0.408] 3.373832e+02 1.226168e+02
## (0.408,0.83] 1.654905e+02 2.945095e+02
## (0.83,0.969] 4.140189e+01 4.185981e+02
## (0.969,0.999] 4.725877e+00 4.552741e+02
## (0.999,1] 1.296203e-01 4.598704e+02wilcox.test(modele.reg.log$fitted.values ~ Don_spam$spam, alternative = c("two.sided"))##
## Wilcoxon rank sum test with continuity correction
##
## data: modele.reg.log$fitted.values by Don_spam$spam
## W = 114390, p-value < 2.2e-16
## alternative hypothesis: true location shift is not equal to 0Le test de Mann-Whitney, basé sur les rangs, nous assure avec une p-value très faible (p-value < 2.2e-16) le rejet de H0. En clair, les distributions sont décalées et donc les scores permettent de distinguer les positifs des négatifs. Ce qui vient renforcer la bonne impréssion faite par le diagramme de fiabilité et l’histogramme de répartition des \(P_β(x_i)\).
Pour conclure sur ces deux tests, ils nous permettent de vérifier des hypothèses sur les \(P_β(x_i)\).Ils ne permettent pas de conclure de la qualité de prédiction mais peuvent servir à justifier de la validité du modèle.
Matrice de confusion
Après avoir visualisé et analysé les scores \(P_β(x_i)\), il est temps de voir à quel point le modèle est juste ou faux. Nous allons voir à travers quelques indicateurs, la performance du modèle.
# matrice confusion
score <- ifelse(predict(modele.reg.log,Don_spam,type="response") >.5, "spam","mail")
confusion.mat = table(Don_spam$spam, score)
fauxneg = confusion.mat[2,1]
fauxpos = confusion.mat[1,2]
vraisneg = confusion.mat[1,1]
vraispos = confusion.mat[2,2]
txerr = (fauxneg+fauxpos) / dim(Don_spam)[1]
sensibilite <- vraispos / (vraispos + fauxneg)
precision <- vraispos / (vraispos + fauxpos)
specificite <- vraisneg / (vraisneg + fauxpos)
confusion.mat## score
## mail spam
## 0 2666 122
## 1 194 1619 data.frame(txerr,sensibilite, precision, specificite)## txerr sensibilite precision specificite
## 1 0.06868072 0.892995 0.9299253 0.956241- la sensibilité ou le rappel nous indique la capacité à trouver les vrais positifs.
- la précision est la proportion de vrais positifs parmis les positifs.
- la spécificité est la proportion de négatifs detectés.
- le taux d’erreur global est l’ensemble des mals classés.
Pour ce modèle, comprenant tous les descripteurs, nous obtenons un taux d’erreur de 6.87 % (les mals classés).
Courbe ROC
La courbe ROC représente la sensibilité (taux de vrais positifs) en fonction de la spécificité (taux de faux positifs) quand on fait varier le seuil ‘s’ (les valeurs des scores). Dans le meilleur des cas (classifieur parfait), la courbe passe par les points (0, 0) à (0, 1) à (1, 1). Si le classifieur s’avère pas mieux que de l’aléatoire, les points sont une bissectrice (0, 0) à (1, 1).
library(ROCR)
pred=prediction(modele.reg.log$fitted.values,Don_spam$spam)
perf=performance(pred,"tpr", "fpr")
auc_ROCR <- performance(pred, measure = "auc")
auc_ROCR <- round(auc_ROCR@y.values[[1]],3)
plot(perf,colorize = TRUE) 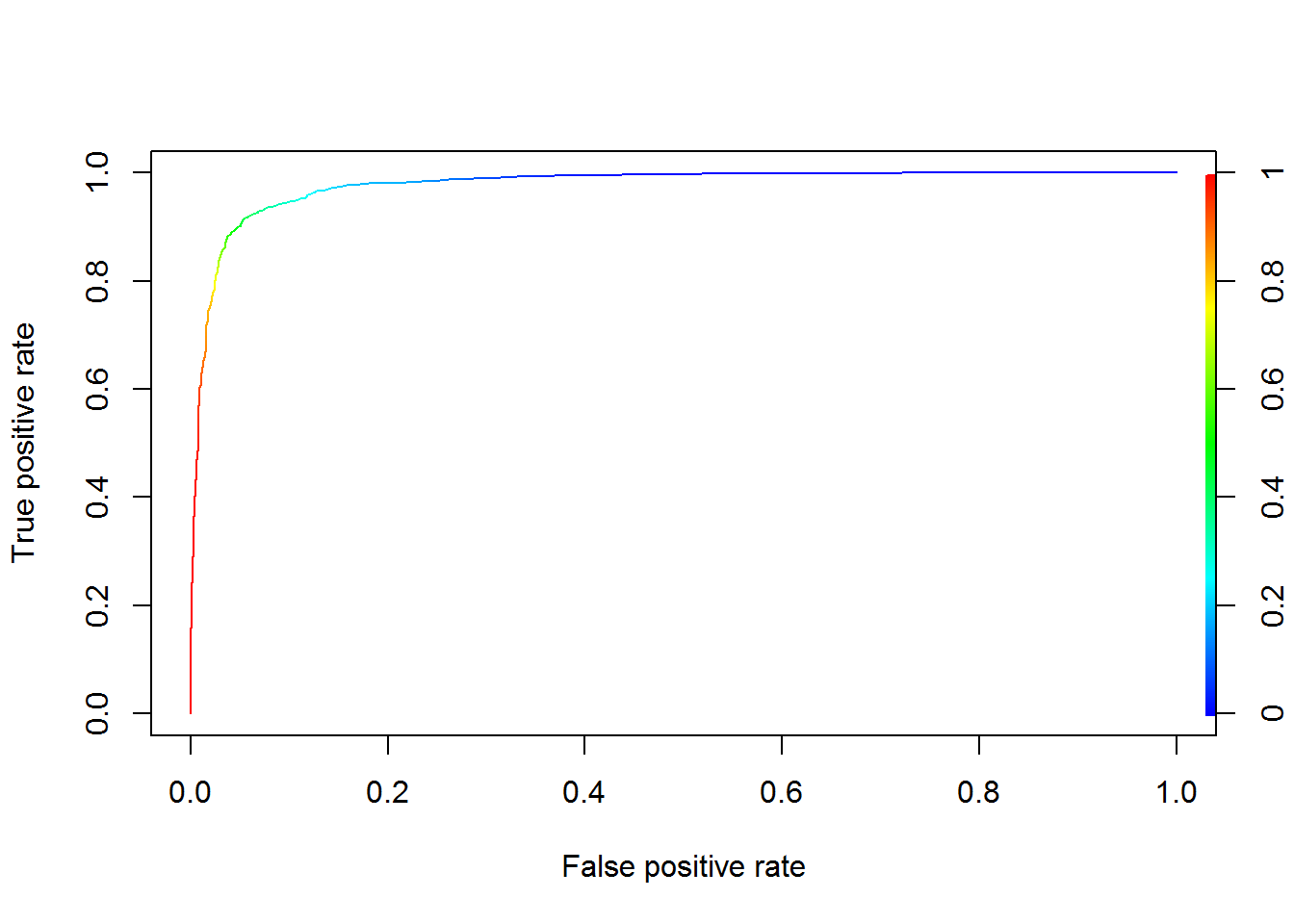
Pour cet exemple, la courbe ROC décrit un classifieur presque parfait (AUC=0.977), n’oublions pas que nous utilisons le même fichier pour l’apprentissage et le test. Nous sommes dans un cas de surapprentissage.
Tests des coéfficients
Maintenant que nous avons évalué le modèle dans sa globlité, revenons sur le comportement asymptotique de l’estimateur du maximum de vraisemblance \(\hat \beta\).
Loi asymptotique :
\(\sqrt n(\hat \beta-\beta)\xrightarrow{{\mathcal{L}}}N(0, \mathcal{I(\beta)^{-1}})\)
\(\mathcal{I}(\beta)\) la marice d’information de Fisher au point \(\beta\).
On en déduit :
\((\hat \beta-\beta)'n\mathcal{I(\beta)^{-1}}(\hat \beta-\beta)\xrightarrow{{\mathcal{L}}}\chi^2_{p+1}\)
Par convergence (\(\hat\beta\) converge faiblement vers \(\beta\)) de l’estimateur, on peut écrire :
\((\hat \beta-\beta)'\hat\Sigma^{-1}(\hat \beta-\beta)\xrightarrow{{\mathcal{L}}}\chi^2_{p+1}\)
avec \(\hat\Sigma^{-1}=(X'W_\hat\beta X)^{-1}\) inverse de la matrice hessienne.
Où \(W_{\hat \beta}\) est la matrice diagolane \(P_{\beta}(x_{i})*(1-P_{\beta}(x_{i}))\)
- Le test de Wald.
- Le test du rapport de vraissemblance (ou déviance).
- Le test du score.
On formule les hypothèses :
\(H_0:\beta_{j1}=\beta_{j2}=...=\beta_{jq}=0 \space contre \space H_1:\exists k \in \{1,2,...,q\}:\beta_{jk}\neq 0\)
Test de Wald :
On note \(\beta_{0,...,q-1}\) le vecteur des q premières composantes de \(\beta\).
Sous \(H_0\), on a :
\(\beta'_{0,...,q-1} \hat\Sigma^{-1}_{0,...,q-1}\beta_{0,...,q-1}\xrightarrow{{\mathcal{L}}}\chi^2_q\)
Test du rapport de vraissemblance :
Le test est basé sur la différence du rapport de vraissemblance entre le modèle et le modèle sous \(H_0\).
Sous \(H_0\), on a :
\(2(\mathcal{L}_{n}(\hat\beta)-\mathcal{L}_{n}(\hat\beta_{H_0}))\xrightarrow{{\mathcal{L}}}\chi^2_{q}\)
Test du score :
Le test vérifie, sous \(H_0\) si la fonction de score (gradient de la log-vraisemblance) est proche de 0.
Sous \(H_0\), on a :
\(S(\hat \beta_0)'\hat\Sigma^{-1}_{H_0}S(\hat \beta_0)\xrightarrow{{\mathcal{L}}}\chi^2_{q}\)
Test de Wald
Le test de Wald est le test qui est implémenté dans la fonction glm {stats}. Contrairement aux deux autres tests, le test de Wald n’a besoin que de la matrice hessienne généré lors de l’obtention du modèle. Il n’a pas besoin de comparer des sous modèles (sous \(H_0\)) et permet donc une execution plus rapide. Neammoins, le test de Wald est plus conservateur et favorise l’hypothèse nulle \(H_0\). L’estimateur repose sur des propriétés asymptotiques et peut s’avérer peut précis sur des petits effectifs.
Application du test de Wald :
L’hypothèse de test pour le modèle (un test de nullité pour chaque variable) :
\(H_0:\beta_{j}=0 \space contre \space H_1:\beta_{j}\neq 0\)
Sous \(H_0\), la statistique de test s’écrit :
\(W(j)=\hat a'(j)\hat\Sigma^{-1}_{j}\hat a(j)\xrightarrow{{\mathcal{L}}}\chi^2_{1}\)
ou
\(Z_j=signe(a'(j))*\sqrt W_j\sim N(0,1)\) (implémenté de cette manière dans glm {stats}).
A partir de la matrice hessienne du modèle, vérifions les p-value :
#test de wald :
V=diag(modele.reg.log$fitted.values*(1-modele.reg.log$fitted.values)) #diagonale des poids
const=rep(1,4601)
X=data.matrix( data.frame(const,Don_spam[,-58]) )
H = t(X) %*% V %*% X ; #matrice hessienne H p*p
inverse.h = solve(H)
modele.reg.log$coefficients[1:4]## (Intercept) wf_make wf_address wf_all
## -1.5686144 -0.3895185 -0.1457768 0.1141402 #prenons wf_make wf_address wf_all
coef=modele.reg.log$coefficients[2:4]
var.cov=inverse.h[2:4,2:4]
z.vect=(coef^2)/diag(var.cov)
pval.wald=c()
#resultat du test khi2
for(i in 1:length(coef)){
pval.wald[i] = 1- pchisq(z.vect[i],1)
}
#R est implémenté avec le test sur N(0,1)
z.vect=abs(coef/sqrt(diag(var.cov)))
pval.norm=c()
#resultat du test N(0,1)
for(i in 1:length(coef)){
pval.norm[i] = 2*(1- pnorm(z.vect[i],0,1))
}
pval.wald ; pval.norm ## [1] 0.09238803 0.03536189 0.30075971## [1] 0.09238803 0.03536189 0.30075971 summary(modele.reg.log)[["coefficients"]][,4][2:4]## wf_make wf_address wf_all
## 0.09238799 0.03536157 0.30075945Nous retrouvons bien à partir de la matrice hessienne du modèle les p-value pour les variables wf_make wf_address wf_all avec un test du \(\chi^2\) ou \(N(0,1)\). Avec un seuil à 5%, seule wf_address serait retenue et signifiative.
Distance de Cook
Cette partie résumera les notions de résidu, points leviers et points influents. En effet, nous avons vu precedemment quels étaient les descripteurs les plus significatifs. Interessons nous maintenant à l’analyse des individus.
Par simplicité d’écriture, nous noterons \(p_i=p_\beta(x_i)\)
C’est à travers la notion de résidu que l’analyse des individus peut se faire. Il existe plusieurs sortes de résidus, le plus simple étant \(Y-\hat p_i\) (résidus bruts). Concernant la distance de Cook, nous aurons besoin d’utiliser les résidus de Pearson.
Résidus de Pearson :
\(RP_i=\frac{Y_i-\hat p_i}{\sqrt{\hat p_i(1-\hat p_i)}}\)
\(RP_i\) peut prendre des valeurs négatives élevées dans le cas de faux positifs et des valeurs positives élevées dans le cas de faux négatifs.
library(ggplot2)
modele.influence=influence(modele.reg.log)
pi=modele.reg.log$fitted.values
pear.res=modele.influence$pear.res
ggplot(Don_spam, aes(x=pi, y=pear.res, color=score) ) +
geom_point(size = 2, aes(shape = Don_spam$spam))+ylim(-10, 10) +
geom_hline(yintercept=c(-2,2), linetype="dashed", color = "red") +
ggtitle("Résidus de Pearson") +
theme(plot.title = element_text(hjust = 0.5))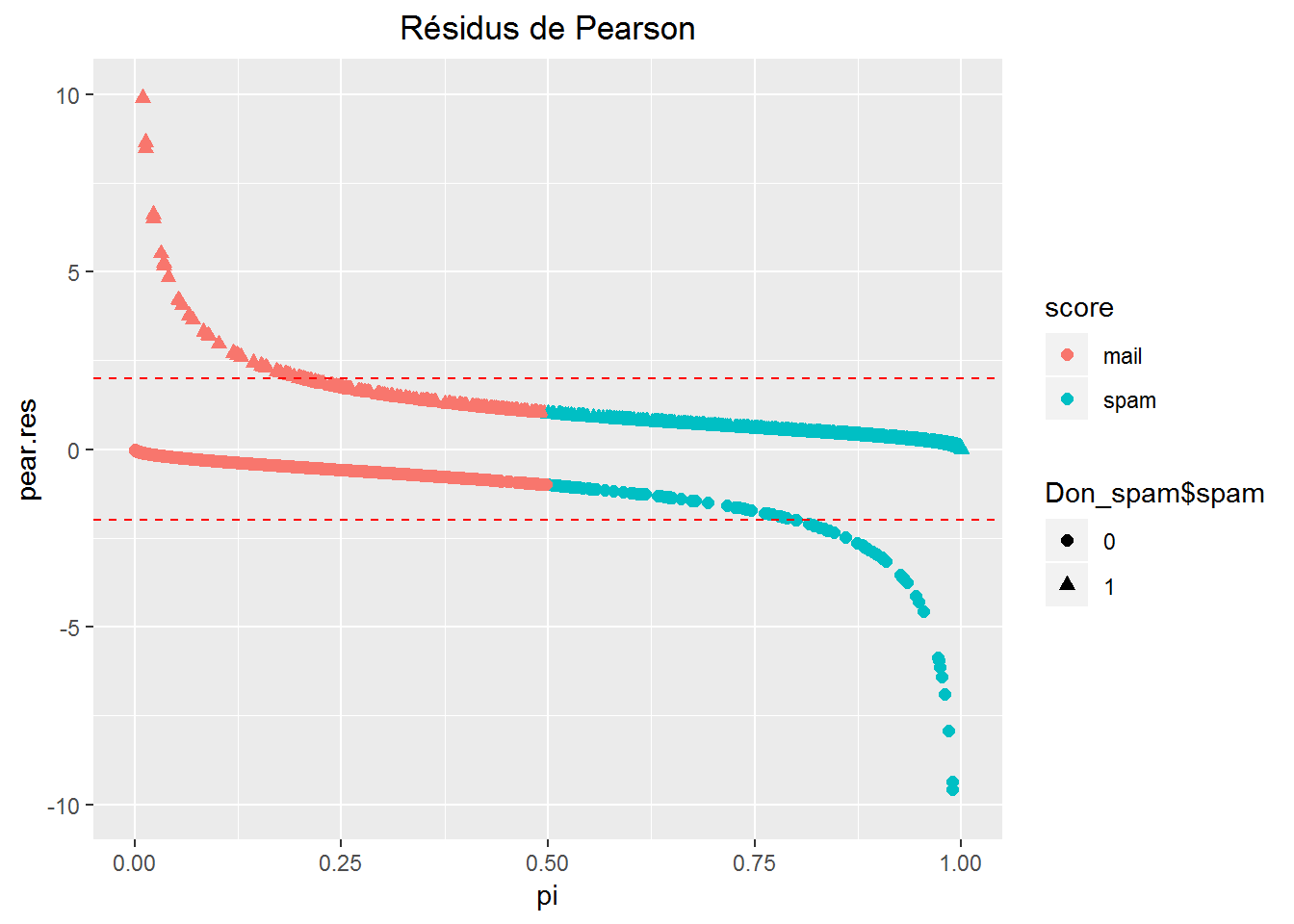
On constate bien les valeurs extrêmes des \(RP_i\), pour les faux négatifs (\(p_i\) faibles pour \(Y=1\)) et les faux positifs (\(p_i\) fortes pour \(Y=0\)).
Points leviers :
Le levier d’une obervation \(x_i\) compare l’écart entre l’observation et les autres observations. Cette mesure permet de détecter un point comme étant atypique. La mesure du levier est défini à partir de la hat matrice ou matrice de projection.
Matrice de projection :
\(H=X(X'W_\hat\beta X)^{-1})X'W_\hat\beta\)
Où \(W_{\beta}\) est la matrice diagolane \(P_{\beta}(x_{i})*(1-P_{\beta}(x_{i}))\).
Pour une observation \(x_i\), le levier est lu sur la diagonale (\(H_{ii}\)).Le levier mesure également l’influence globale d’un point sur la prédiction des valeurs \(\hat p_i\). Cette influence est l’influence globale du point \(x_i\) sur la prédiction des valeurs de tout autre point \(x'_i\).
Points influents :
Un point est dit influent si il influe sur la valeur des coefficients \(\beta\). Cette mesure est possible à condition de calculer la distance entre un coefficient estimé avec toutes les observations et un coefficient mesuré avec toutes les observations sauf une. Une mesure courante de cette influence est la distance de Cook.
Distance de Cook :
La distance de Cook pour un individu s’écrit :
\(D_i=\frac{1}{p}(\hat \beta_i - \hat \beta)'X'W_{\hat \beta}X(\hat \beta_i - \hat \beta)\approx \frac{rp^2_i*H_{ii}}{p(1-H_{ii})}\)
Avec
\(p=\sum_iH_{ii}\) et \(rp_i^2\) le résidus de Pearson au carré.
Dans la première partie du calcul de la distance de Cook, il nous faut calculer n sous modèles. Ce n’est pas très bon en terme d’optimisation et c’est pour cela que le levier intervient \(D_i\approx \frac{rp^2_i*H_{ii}}{p(1-H_{ii})}\).
Il existe un seuil, qui s’écrit :
\(D_i>\frac{4}{n-p-1}\) avec \(n\) le nombre d’observations et \(p=p+1\) variables.
p=sum(modele.influence$hat) # p=p+1
seuil.cook = 4 / (dim(Don_spam)[1] - p) #4/(p+1-1) = 0.0008804755
individus.spam = rownames(Don_spam)
library(gridExtra)
x=1:4601 ; y.cook=as.vector(cooks.distance(modele.reg.log)) ; classe=Don_spam$spam
gg.cook = ggplot(Don_spam, aes(x=x, y=y.cook, fill = classe, colour=classe) ) +
geom_bar(stat = "identity") +
geom_text( aes(label = ifelse(as.vector(cooks.distance(modele.reg.log)) > 50*seuil.cook, individus.spam, ""))) +
geom_hline(yintercept=seuil.cook, linetype="dashed", color = "red") +
geom_text(aes( 0, seuil.cook, label = round(seuil.cook,digits=3), vjust = -1), size = 4)+
ggtitle("Di de Cook gobal") +
theme(plot.title = element_text(hjust = 0.5))#pb d'echelle sans ylim
#remise à l'échelle
gg.cook.detail = ggplot(Don_spam, aes(x=x, y=y.cook, fill = classe, colour=classe) ) +
geom_bar(stat = "identity") +
geom_text( aes(label = ifelse(as.vector(cooks.distance(modele.reg.log)) > 50*seuil.cook, individus.spam, ""))) +
geom_hline(yintercept=seuil.cook, linetype="dashed", color = "red") +
geom_text(aes( 0, seuil.cook, label = round(seuil.cook,digits=3), vjust = -1), size = 4) +
coord_cartesian(ylim=c(0,0.009))+
ggtitle("Di de Cook détail") +
theme(plot.title = element_text(hjust = 0.5))#pb d'echelle sans ylim
grid.arrange(gg.cook, gg.cook.detail, ncol=2, nrow = 1)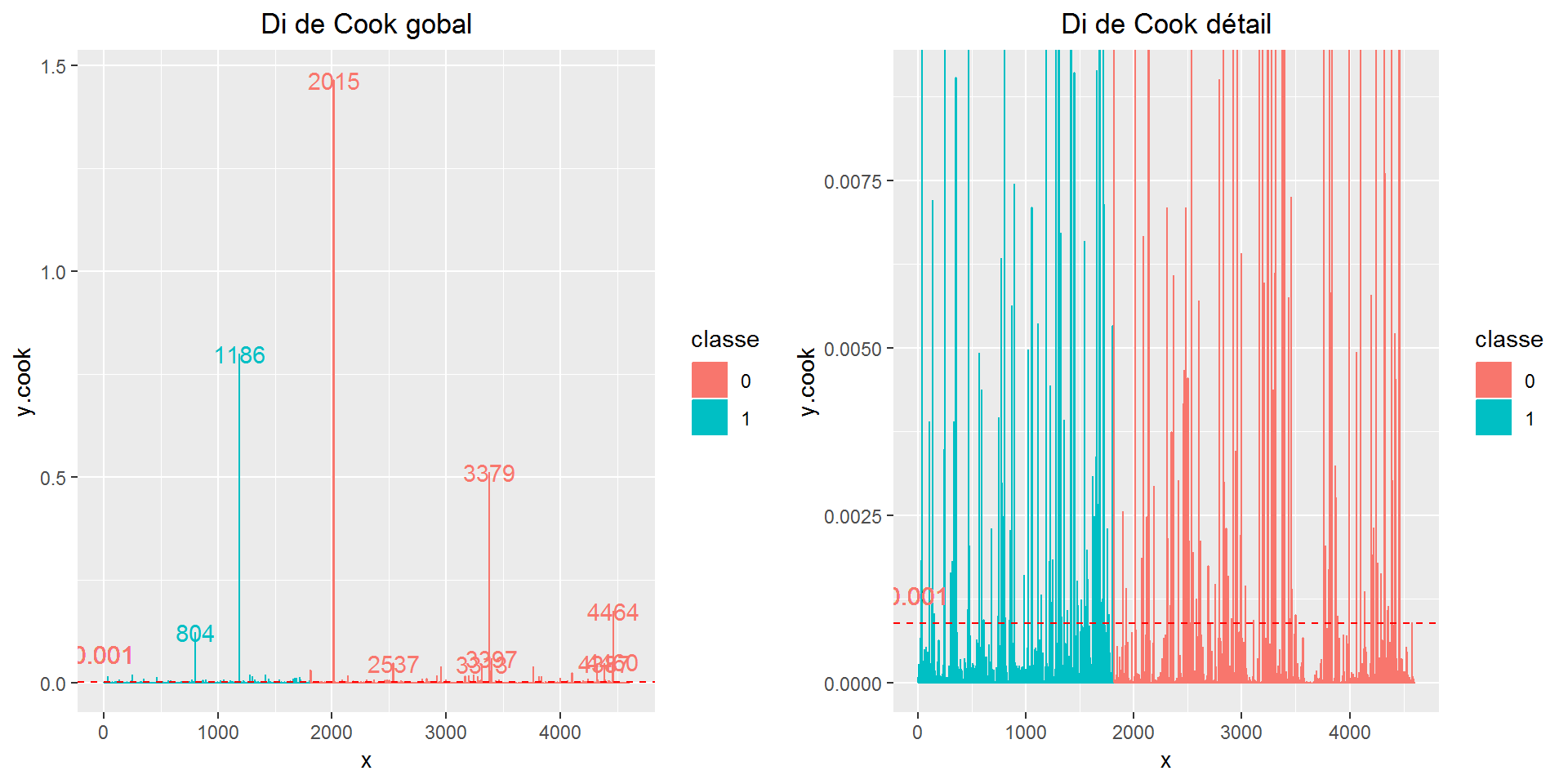
#comptage du nombre d'individus hors seuil
hors.seuil.cook = y.cook[which(y.cook > seuil.cook)] #valeurs decroissantes des individus leviers
length(hors.seuil.cook) #209 individus ## [1] 209Sur le graphique de gauche, le seuil parait infime, mais c’est parce que nous avons des valeurs extremes du \(D_i\) de Cook. Le graphique de droite, avec une échelle ajustée, permet de voir qu’il y a de nombreux individus hors seuils. Cependant cela ne représente que 209 individus, soit 4.5% des individus au total.
Je n’ai pas refait ici un modèle sans les individus hors seuil de cook mais cela améliore de façon significative le taux d’erreur (mals classés) sur le train.
Cette partie “Evaluation du modèle” est terminée, maintenant que nous connaissons mieux la nature du modèle de régression logistique, nous allons pouvoir appliquer des données “test” pour la prédiction.
Application sur échantillon TEST
Cette partie est consacrée à la prédiction, pour cela nous allons créer un échantillon d’apprentissage et un échantillon test(individus à prédire). Pour rappel le fichier “spam” est composé de 4601 individus et 57 descripteurs ainsi que la variable classifiante binaire (“spam” : 1 “mail” : 0).
Dans cette partie, nous allons uniquement nous concentrer sur le “taux d’erreur global” (les mals classés fauxpos+fauxneg/n). Egalement cette partie aura pour objectif de comparer le taux d’erreur d’un modèle complet (toutes les variables), d’un modèle sans les individus “hors seuils de Cook” et d’un modèle avec sélection automatique de variables (stepAic).
Nous allons répeter l’expérience et génerer 100 échantillons d’apprentissage et 100 échantillons test. A chaque itération, les individus servant à costruire l’échantillon d’apprentissage ne se retrouve pas dans l’échantillon test et inversement.
La procédure stepAIC {MASS} étant longue à éxecuter, l’expérience se fera sur 10 éssais.
Modèle complet :
Création d’un modèle à partir de tous les descripteurs et application sur échantillon test.
Modèle hors seuils de Cook :
C’est à partir du modèle complet qu’il est possible de calculer les \(D_i\) de Cook pour ensuite enlever les individus hors seuils (\(D_i>\frac{4}{n-p-1}\)). Nous appliquons ensuite l’échantillon test sur ce modèle privé des individus hors seuils.
Modèle stepAic :
Tout d’abord la procédure stepAIC {MASS} permet, de façon automatique, de sélectionner les descripteurs du modèle. C’est également à partir des résultats d’un premier modèle (objet glm() en paramètre) que la procedure stepAic peut être utilisée. Pour résumer, la procédure stepAic utilise une méthode de sélection de variables (ici de type “both”) et cherche à minimiser l’AIC du modèle. En sortie nous avons donc un modèle de type glm, comprenant uniquement les descripteurs minimisant le critère AIC (en général \(p_{aic}<p\), avec p descripteurs au départ).
Nous allons donc comparer les 3 modèles à travers les taux d’erreur sur les échantillons test.
⚠⚠⚠
Attention aux modèles abérrants !
En effet, pour certains échantillons d’apprentissage, nous pouvons obtenir :
-
Une déviance plus élevée que la déviance du modèle trivial (avec des valeurs pour les coéfficients de l’ordre de 10^14 ou même à
NA) sur le modèle par défaut. - Le modèle sans les individus hors seuil de Cook peut devenir abérrant pour les mêmes raisons (peut devenir abérrant même à partir d’une modèle non abérrant).
Ces modèles abérrants sont écartés de l’analyse. En moyenne, cela impacte significativement le taux d’erreur des modèles hors seuil de Cook.
⚠⚠⚠
Comportements moyens des modèles :
seed=1423
mat.verif=c();mat.verif.cook=c()
tx_err.cook=c();tx_err=c()
for(i in 1:100){
#initialisation du seed
set.seed(seed+i)
#generation de l'echantillon TRAIN
#rappel proportion au global "email 61%" "spam 39%"
trainIndex <- sample(index, trunc(length(index) * 0.666666666666667))
DATASET.train <- Don_spam[trainIndex, ]
#generation de l'echantillon TEST
DATASET.test <- Don_spam[-trainIndex, ]
#####
#REGRESSION SUR TOUTES LES VARIABLES
#####
##TRAIN
modele.defaut = glm(DATASET.train$spam ~ .,
family = binomial(link="logit"), data=DATASET.train)
####
# controle du modèle
####
# valeurs NA dans les coeff
# modele.defaut$coefficients ; is.na(modele.defaut$coefficients)
iter.na=0
if(anyNA(modele.defaut$coefficients)){ # NA {base}
iter.na = seed+i
}
# deviance residuelle > deviance modèle trivial
iter.bug.dev=0
if(modele.defaut$deviance >= modele.defaut$null.deviance){
iter.bug.dev = seed+i
}
####
# les seed à éliminer
####
if(iter.na > 0 || iter.bug.dev > 0){
mat.verif = rbind(mat.verif, c(iter.na, iter.bug.dev))
}
####
# si pas de NA dans les coeff et pas de deviance aberante
####
else {
# 1 - prediction sur le test a partir du modèle
pred.test = ifelse(predict(modele.defaut,DATASET.test,type="response") >.5, 1,0)
#cbind(predict(modele.defaut,DATASET.test,type="response"), pred.test) pour controle
confusion.mat = table(DATASET.test$spam, pred.test)
tx_err[i] = (( confusion.mat[1,2] + confusion.mat[2,1] ) /
dim(DATASET.test)[1] )*100
# 2 - Traitement des individus hors seuils cook
# a partir du modele par defaut
#distance de cook et seuil
train.cook = cooks.distance(modele.defaut)
p.hat.train=sum(influence(modele.defaut)$hat) #les 57 variables + 1
seuil.cook.train = 4 / (dim(DATASET.train)[1] - p.hat.train)
######
#REGRESSION SANS LES HORS SEUILS COOK du TRAIN
######
##NOUVEAU TRAIN
DATASET.train.cook = DATASET.train[-which(train.cook > seuil.cook.train),] #suppréssion des hors seuil pour nouveau train
#dim(DATASET.train) ; dim(DATASET.train.cook) pour controle
#modele sur le nouveau train
modele.cook = glm(DATASET.train.cook$spam ~.,
family = binomial(link="logit"), data=DATASET.train.cook)
####
# Controle du modèle
####
## test du modele NA et deviance aberante
if(anyNA(modele.cook$coefficients)){ # NA {base}
iter.na = seed+i
}
# deviance residuelle > deviance modèle trivial
iter.bug.dev=0
if(modele.cook$deviance >= modele.cook$null.deviance){
iter.bug.dev = seed+i
}
# seed à éliminer
if(iter.na > 0 || iter.bug.dev > 0){
mat.verif.cook = rbind(mat.verif.cook, c(iter.na, iter.bug.dev))
}
####
# si pas de NA dans les coeff et pas de deviance aberante
####
else{
pred.cook = ifelse(predict(modele.cook,DATASET.test,type="response") >.5, 1,0)
#cbind(predict(modele.defaut,DATASET.test,type="response"), pred.test) pour controle
confusion.mat = table(DATASET.test$spam, pred.cook)
tx_err.cook[i] = (( confusion.mat[1,2] + confusion.mat[2,1] ) /
dim(DATASET.test)[1] )*100
}
} # fin modeles ok defaut + cook
}# fin bouclage
summary(tx_err) # modele par defaut
# Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
# 6.128 7.236 7.627 7.599 7.953 9.387 1
summary(tx_err.cook) # modele sans les individus hors seuils cook
# Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
# 5.867 6.747 7.203 7.129 7.432 8.540 30Pour 100 train et 100 test indépendants, nous obtenons :
- Le modèle par défaut : un taux d’erreur moyen de 7.599 %.
- Le modèle sans les individus hors seuil de Cook : un taux d’erreur moyen de 7.129 %.
Concernant les modèles abérrants, nous n’en n’avons qu’un seul pour le modèle par défaut et 30 pour les hors seuil de Cook. Vous trouverez dans le code l’objet contenant la liste des seed responsables.
En moyenne, nous pouvons conclure qu’il semble interessant d’enlever les individus hors seuils de Cook du modèle initial. Cela dit, les résultats sont relativement proches (0.47 % de gain sur le taux d’erreur moyen du modèle par défaut).
Partie stepAIC :
seed=1423
mat.verif.step=c()
tx_err.stepaic=c()
for(i in 1:10){
#initialisation du seed
set.seed(seed+i)
#generation de l'echantillon TRAIN
#rappel proportion au global "email 61%" "spam 39%"
trainIndex <- sample(index, trunc(length(index) * 0.666666666666667))
DATASET.train <- Don_spam[trainIndex, ]
#generation de l'echantillon TEST
DATASET.test <- Don_spam[-trainIndex, ]
#####
#REGRESSION SUR TOUTES LES VARIABLES
#####
##TRAIN
modele.defaut = glm(DATASET.train$spam ~ .,
family = binomial(link="logit"), data=DATASET.train)
####
# controle du modèle
####
# valeurs NA dans les coeff
# modele.defaut$coefficients ; is.na(modele.defaut$coefficients)
iter.na=0
if(anyNA(modele.defaut$coefficients)){ # NA {base}
iter.na = seed+i
}
# deviance residuelle > deviance modèle trivial
iter.bug.dev=0
if(modele.defaut$deviance >= modele.defaut$null.deviance){
iter.bug.dev = seed+i
}
####
# les seed à éliminer
####
if(iter.na > 0 || iter.bug.dev > 0){
mat.verif.step = rbind(mat.verif.step, c(iter.na, iter.bug.dev))
}
####
# si pas de NA dans les coeff et pas de deviance aberante
####
else {
library(MASS)
modele.stepwise = stepAIC(modele.defaut,
trace = TRUE, data = DATASET.train, direction = "both")
#deviance
deviance.train.stepaic[i] = modele.stepwise$deviance
## Prediction sur TEST
pred.stepaic = ifelse(predict(modele.stepwise,DATASET.test,type="response") >.5, 1,0)
confusion.mat = table(DATASET.test$spam, pred.stepaic)
tx_err.stepaic[i] = (( confusion.mat[1,2] + confusion.mat[2,1] ) /
dim(DATASET.test)[1] )*100
}
} # fin bouclage
summary(tx_err.stepaic)
# Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
# 6.714 7.040 7.301 7.613 7.888 9.322 1Nous constatons qu’en moyenne les taux d’erreurs sont du même ordre.
- Modèle complet : 7.599 %.
- Modèle hors seuils de Cook : 7.129 %.
- Modèle stepAic : 7.613 %.
Pour résumer :
- Le modèle complet s’exécute rapidement et obtient un bon résultat.
- Retirer les individus hors seuils de Cook améliore, en moyenne, légerement les résultats.
- La procédure stepAic est très longue et ne semble par améliorer les performances.
A travers cette expérience, nous avons pu voir qu’il n’y a pas de recette miracle pour améliorer le taux d’erreur du modèle. Dans l’absolu il faut un train le plus équilibré possible et surtout sans valeur abérrante.
Cross validation
Il est possible d’évaluer le modèle à travers le taux d’erreur de substitution à l’aide de la validation croisée cv.glm {boot}. Cette méthode est utiliée dans le cas ou nous avons peu de données et donc pas la possibilité d’utiliser des individus test.
######
# Cross validation
######
library(boot)
# Estimation des mal classés par validation croisée :
modele <- glm(spam~ .,data=DATASET.train,family=binomial)
# fonction dit de cout, ici dans le cas d'une variable factorielle
cout <- function(spam,prevision_prob){
return(mean(abs(spam-prevision_prob)>0.5))
}
pi.test=as.vector(modele$fitted.values)
cv.glm(DATASET.train,modele,cout, K=10)$delta
# $K
# [1] 10
#
# $delta
# [1] 0.07433975 0.07332895On obtient ici après une cross validation sur 10 blocs, un taux d’erreur moyen de 7.43 % et une valeur ajustée de cet estimateur de 7.33 %. La cross validation a été effectuée sur le modèle par défaut mais peut être réalisée sur n’importe quel modèle.
On retrouve a peu pres la valeur du taux moyen pour le modèle par défaut éprouvé avec 100 train/test indépendants et aléatoires (7.599 %).
On peut constater que le fichier est composé majoritairement d’emails (“non spam”, 61%)
On note également l’apparition d’un caractère “!” dans les mails de type “spam”